Reading-Notes

Code Fellows Python 401

Read: Data Structure and Analysis - Trees

Binary Trees, Binary Search Trees, and K-ary Trees.

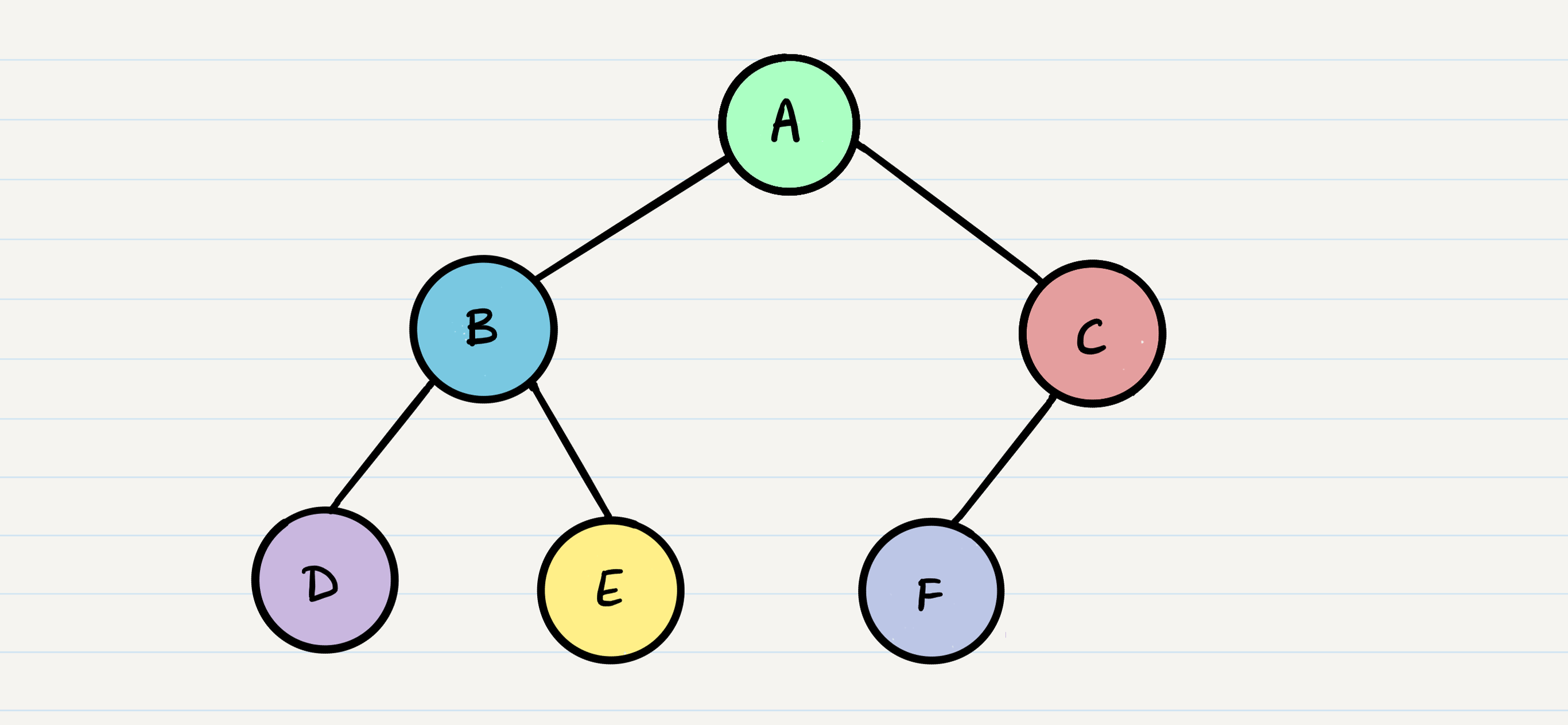
Common Terminology:

Node - A Tree node is a component which may contain its own values, and references to other nodes Root - The root is the node at the beginning of the tree K - A number that specifies the maximum number of children any node may have in a k-ary tree. In a binary tree, k = 2. Left - A reference to one child node, in a binary tree Right - A reference to the other child node, in a binary tree Edge - The edge in a tree is the link between a parent and child node Leaf - A leaf is a node that does not have any children Height - The height of a tree is the number of edges from the root to the furthest leaf

Traversals

how you move/navigate through a tree

• 2 types of traversal:
  • Depth First
  • Breadth First

Depth First

• prioritize going through the depth (height) of the tree
• dif method changes the order in which we search/print the root
• most common way to traverse through a tree is to use recursion

Pre-order: root >> left >> right

ALGORITHM preOrder(root)
// INPUT <-- root node
// OUTPUT <-- pre-order output of tree node's values

    OUTPUT <-- root.value

    if root.left is not Null
        preOrder(root.left)

    if root.right is not NULL
        preOrder(root.right)

output: A, B, D, E, C, F

In-order: left >> root >> right

ALGORITHM inOrder(root)
// INPUT <-- root node
// OUTPUT <-- in-order output of tree node's values

    if root.left is not NULL
        inOrder(root.left)

    OUTPUT <-- root.value

    if root.right is not NULL
        inOrder(root.right)

output: In-order: D, B, E, A, F, C

Post-order: left >> right >> root

ALGORITHM postOrder(root)
// INPUT <-- root node
// OUTPUT <-- post-order output of tree node's values

    if root.left is not NULL
        postOrder(root.left)

    if root.right is not NULL
        postOrder(root.right)

    OUTPUT <-- root.value

output: Post-order: D, E, B, F, C, A

Breadth First

• iterates through the tree by going through each level of the tree

ALGORITHM breadthFirst(root)
// INPUT  <-- root node
// OUTPUT <-- front node of queue to console

  Queue breadth <-- new Queue()
  breadth.enqueue(root)

  while ! breadth.is_empty()
    node front = breadth.dequeue()
    OUTPUT <-- front.value

    if front.left is not NULL
      breadth.enqueue(front.left)

    if front.right is not NULL
      breadth.enqueue(front.right)

output: Output: A, B, C, D, E, F

K-ary Trees

• Nodes are able have more than 2 child nodes
• K refers to the max amount of children in a K-ary Trees

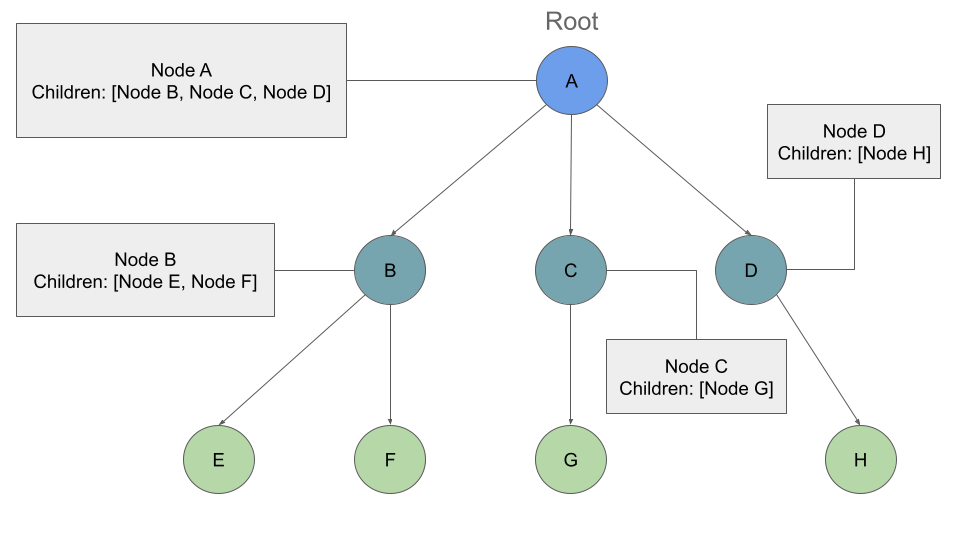
Breadth First Traversal

• moving down a list of children of length k

ALGORITHM breadthFirst(root)
// INPUT  <-- root node
// OUTPUT <-- front node of queue to console

  Queue breadth <-- new Queue()
  breadth.enqueue(root)

  while ! breadth.is_empty()
    node front = breadth.dequeue()
    OUTPUT <-- front.value

    for child in front.children
        breadth.enqueue(child)

Output: A, B, C, D, E, F, G, H

Binary Search Trees

• all values that are smaller than the root are placed to the left, and all values that are larger than the root are placed to the right

Resources

Trees